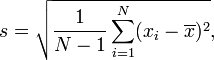I thought to myself, "self, holy crap! That's nasty!" (there are actually a lot of nastier formulae, but I was young in my academic career and hadn't seen too many of them yet). At the time all I did was just memorize the formula and promptly forgot it after I had finished the course.
After I started taking economics and I had to take a lot more statistics, I started to wonder why this equation is the way it is. It turns out to be a bit interesting, and you can learn a bit about statistics when you answer this question.
The part that I thought was the weirdest is that when you take the standard deviation of the population you divide by n, however when you take it from a sample, you use n - 1. Why did the do this?
Let's go on an aside for a bit. When we are using a sample, these statistics that we are generating (the sample mean and the variance) are estimators of the actual parameters, based on the sample that we have taken. These two estimators are random variables, which means it is highly unlikely that they will be the same as the actual parameters. This is not a bad thing, however we would like to have some measures of "goodness" of the estimators that we have.
One measure of "goodness" is called unbiasedness. Intuitively we all know what a bias is, it is something that sorta skews the estimate away from the actual value that we are estimating. Formally you would call the estimator unbiased if:
E(estimator) = parameterThe E function there is the expected value of the random variable, which is essentially an average value that the random variable comes out to. If on average the estimator is not coming out to be our parameter, then we have some kind of bias going on.
Given the above definition, our variance estimator would be unbiased if:
E(s2) = σ2It turns out that if you divide by n for the sample variance you end up with:
E(s2) = &sigma2 * (n - 1) / nThis is always smaller than the variance, so our estimate is biased downwards. Thus we must correct the bias by dividing by n - 1 instead of n.
So that's why you divide by n - 1 and not n. While that's almost enough statistics for you for one day, there is one last tidbit of information that can be taught here. If you look at the formula for the expected value of the biased estimator, you'll notice that the bias will shrink as n gets large. In fact in the limit, the bias will go to zero and you will have an unbiased estimator. The name for this type of estimator is a consistent estimator. While they are not as good as unbiased estimators (note that all unbiased estimators are consistent), it is often the case that you might want to use a biased yet consistent estimator instead of an unbiased one if perhaps there is something wrong with the variance of the unbiased estimator. Eventually in one of my statistics posts I will talk about some problems with real-world data that might cause this sort of thing to happen.